Discussion | evo-roadtrips

A possible explanation for such a result comes from the lack of direct connections between the attraction points and the roads. Indeed, no roads lead to the attraction points and this means that the attraction points themselves, although close to the roads, may be surrounded by high friction zones (Non-driving zones), which means that the Least Cost Path will not be forced to go to these points.

Therefore, it is necessary to find a strategy which would create a more accurate Least Cost Path which would be “forced” to go through the attraction points.

One possible way to force the path to go through the points could be to create connections between the attraction points and the Network Junctions created by the Network Analyst. Such could perhaps link the points to the roads, and allow the path to go through them.

Nevertheless, it is also important to consider using just the Network analyst to fix this problem. In order to do so, several attraction points, let’s assume the most popular points, would be pre selected as stop points. These stops would be added as Stops in the Route analysis generated by the Network Analyst, and the shortest route going through these points could then be calculated.

Indeed, the Route Solver within the Network Analyst is a way to solve this “Travelling Salesman Problem” assuming we have selected a combination of Stops (attraction points) the route has to go through to the final destinations from downtown vancouver. Within the route solve it would be required to “Reorder Stops To Find Optimal Route option” in order to set the order of stops to the final stop. (Kronicz, JD. “5.1 Network Analysis.” 5.1 Network Analysis | GEOG 497C: Transportation GIS, www.e-education.psu.edu/geog497c/node/647.)

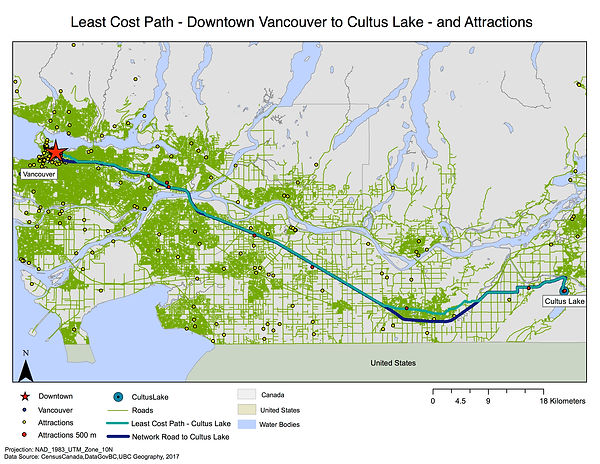
The shortest path from Downtown Vancouver to Whistler, Cultus Lake, Deep Cove, and Harrison Hot Springs have been calculated through different ways. The shortest routes have been calculated through a vector based method using a network analysis. The shortest distances going through attractions points were calculated using a raster based approach by creating a cost surface and least cost paths.

The Least Cost Path has shown its usefulness in a GIS analyses in finding a path that would result in the cheapest roads for EVO users. Nevertheless, there are some limitations to the conclusions found from the analysis.

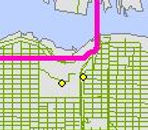
In fact, if we look at the Least Cost Path map for Cultus Lake and Harrison Hot Springs, it is possible to observe that the two calculated paths are not the same. Indeed, if you look at the example below, the Least Cost Path Line is different that the Network dark blue line.

If we look more closely it is interesting to notice that while indeed the Least Cost Path appears to be shorter, it seems that the network road actually goes through more attraction points. Consequently, this points out a potential issue in the calculation of the Least Cost Paths.

Discussion, Limitations and Potential Solutions

Furthermore, if we look at the screenshot below from the Deep Cove Least Cost Path, it is possible to observe that the pink line did not make a detour to go through the two attraction points, which were not far from the final road.